Probe Harness for Platinum Resistance Sensor
Different connection methods of PT100/PT1000/PT500/PT200 platinum resistance temperature sensor probe harness. Temperature is a very important physical quantity in work control. Sensors used for temperature measurement mainly include thermal resistors, thermistors, thermocouples, semiconductor temperature sensors, etc. Each of these sensors has its own characteristics and applicable fields, and designers must choose the appropriate sensor based on their specific applications.
A resistor thermal detector (RTD) is a highly accurate temperature sensor that uses thin metal wires wrapped around a bracket to form a resistor whose resistance changes with temperature. The operating temperature range is -200℃~+850℃. Common RTD materials include nickel, copper, platinum, etc., among which 100Ω (at 0°C) platinum thermal resistors are the most common. Since the physical and chemical properties of platinum metal are very stable, platinum resistors are widely used due to their high precision, good long-term stability, good repeatability, and fast response.
The following formula describes the temperature characteristics of Pt100. It can be seen from the formula that the temperature and resistance characteristics of Pt100 are obviously nonlinear. However, compared with thermocouples and thermistors, the linearity of Pt100 is much better, so nonlinear correction is relatively easy. Early nonlinear corrections were mostly implemented using complex analog circuits. With the development of electronic technology, in current practical applications, microcontrollers are generally used to perform nonlinear correction of Pt100 using table lookup combined with interpolation.
Since the thermal resistor is a passive device, it requires external stimulation to work during use. During use, attention must be paid to the appropriate size of the excitation current. Excessive current will cause Pt100 to heat itself, resulting in measurement errors. Therefore, the signal conditioning circuit must be carefully designed according to the measurement requirements during the design process to ensure that the error caused by the sensor's own heating is within the acceptable range.
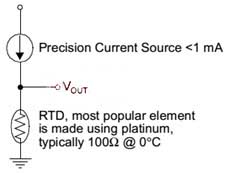1. Why use three-wire and four-wire connection methods?
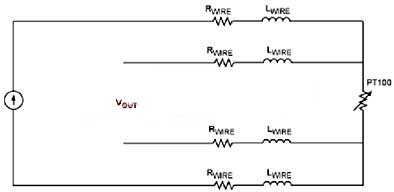
Since the temperature coefficient of Pt100 is only 0.385Ω/℃, if the distance between the sensor and the controller is long and a long lead is required, the measurement error due to lead resistance may be serious. For example, assume there is a Pt100 connected to the controller via 100 feet (approximately 30 meters) of 30 gauge copper leads. The resistance of 30 gauge copper wire is 0.105Ω/ft. If the conventional two-lead connection method is used, as shown in the figure below, a total resistance of 21Ω will be generated on the leads, which is equivalent to a measurement error of 55!
To solve this problem, in addition to the two-wire connection method, Pt100 also has three-wire and four-wire connection methods to reduce or even eliminate the measurement error caused by lead resistance.
2. Two-, three- and four-wire connection methods for constant current source excitation
As mentioned above, Pt100 is a resistive temperature sensor, and the essence of its temperature measurement is actually to measure the resistance of the sensor. The usual approach is to convert resistance into electrical signals such as voltage or current for measurement, and then use a microcontroller to linearize the measurement results. Generally, there are two options for temperature measurement using Pt100:
1. Design a constant current source to pass through the Pt100 thermal resistor, and calculate the temperature by detecting the voltage on the Pt100;
2. Use Wheatstone bridge. Three of the four resistances of the bridge are constant, and the other one uses a Pt100 thermal resistor. When the resistance value of Pt100 changes, an electric-heat difference will be generated at the test end, and the temperature is calculated from the electric-heat difference.
There is also a type of measurement method called "proportional method", which can be regarded as an improvement of the first type of measurement method and will be introduced in detail later.
The connection method of the 2-wire constant current source excitation is shown in the figure below. Pass the constant current source output through Pt100, measure the voltage across Pt100 and convert it into temperature. As mentioned before, this connection method will cause large errors when the Pt100 lead is long. Therefore, the more practical methods in actual applications are three-wire and four-wire connections.
The 4-wire connection method (Kelvin connection method) is shown in the figure below. Use two different sets of leads to lead out the excitation and measurement ends of Pt100. Since the voltage measurement point is at the lead connection of Pt100, the lead excitation voltage will not affect the measurement results.
The four-wire connection method is widely used in laboratory temperature measurement due to its high accuracy. However, due to constraints such as cost and wiring convenience, the three-wire connection method is more widely used in industrial control sites.
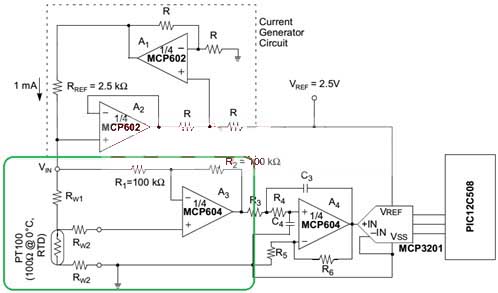
The figure below shows a typical connection method of a three-wire Pt100 excited by a constant current source. The basic principle is to assume that the three leads of Pt100 use the same type of cable with the same length and have the same resistance value, that is, Rw1=Rw2=Rw3 in the figure below, and use the measurement end (Rw2 lead) to compensate for the lead resistance.
Specifically, for the connection in the figure, the voltage at the non-inverting input terminal of op amp A3 is V+=Vpt100+VRw3, and the voltage at the inverting input terminal of op amp A3 is V-=VRw1 + Vpt100 + VRw3. Based on the assumption that Rw1=Rw2=Rw3, there is Vrw1 = Vrw3. Then the output Vo of op amp A3 = 2V+ - V- = Vpt100. That is to say, the influence of lead resistance on the measurement results is theoretically eliminated.
3. Two- and three-wire connection methods of Wheatstone bridge
The Wheatstone bridge is another common connection method for Pt100. Its two-wire connection method is shown in the figure below. Obviously when the Pt100 lead is longer, larger errors will be introduced.
The three-wire Pt100 Wheatstone bridge connection method is shown in the figure below. The output formula of the Wheatstone bridge is as follows. If R3=Rpt100 is selected, the measurement error caused by the lead resistance can be theoretically eliminated.
4. 2, 3, and 4-wire connection methods in proportional method measurement
The essence of the proportional method measurement is to connect Pt100 in series with a reference resistor and apply an excitation source. Since the current flowing through the Pt100 and the reference resistor is the same, the voltage ratio between the two is the ratio of the resistance values. Taking the voltage across the reference resistor as the AD converter reference voltage and performing AD conversion on the voltage across the Pt100, there is the formula where D is the ADC conversion result and N is the number of ADC bits.
Since the current flowing through the Pt100 and the reference resistor is the same, compared with the above two structures, this circuit has lower requirements for the excitation source. Due to its simple structure, few precision components, and high measurement accuracy, proportional method measurement circuits are recognized by more and more people.
The figure below shows the proportional two-wire Pt100 connection method. Obviously when the Pt100 lead is longer, larger errors will be introduced.
In this circuit, the two-wire Pt100 can be directly replaced with the four-wire Pt100 and changed to a four-wire connection to eliminate lead errors.
The figure below shows the proportional three-wire Pt100 connection method. Use two constant current sources with equal outputs to compensate for lead resistance.
 |
 |
| Platinum resistance sensor wire harness from China | Platinum Resistance Sensor Wire Harness and Connector |
A resistor thermal detector (RTD) is a highly accurate temperature sensor that uses thin metal wires wrapped around a bracket to form a resistor whose resistance changes with temperature. The operating temperature range is -200℃~+850℃. Common RTD materials include nickel, copper, platinum, etc., among which 100Ω (at 0°C) platinum thermal resistors are the most common. Since the physical and chemical properties of platinum metal are very stable, platinum resistors are widely used due to their high precision, good long-term stability, good repeatability, and fast response.
The following formula describes the temperature characteristics of Pt100. It can be seen from the formula that the temperature and resistance characteristics of Pt100 are obviously nonlinear. However, compared with thermocouples and thermistors, the linearity of Pt100 is much better, so nonlinear correction is relatively easy. Early nonlinear corrections were mostly implemented using complex analog circuits. With the development of electronic technology, in current practical applications, microcontrollers are generally used to perform nonlinear correction of Pt100 using table lookup combined with interpolation.
Since the thermal resistor is a passive device, it requires external stimulation to work during use. During use, attention must be paid to the appropriate size of the excitation current. Excessive current will cause Pt100 to heat itself, resulting in measurement errors. Therefore, the signal conditioning circuit must be carefully designed according to the measurement requirements during the design process to ensure that the error caused by the sensor's own heating is within the acceptable range.
Since the temperature coefficient of Pt100 is only 0.385Ω/℃, if the distance between the sensor and the controller is long and a long lead is required, the measurement error due to lead resistance may be serious. For example, assume there is a Pt100 connected to the controller via 100 feet (approximately 30 meters) of 30 gauge copper leads. The resistance of 30 gauge copper wire is 0.105Ω/ft. If the conventional two-lead connection method is used, as shown in the figure below, a total resistance of 21Ω will be generated on the leads, which is equivalent to a measurement error of 55!
To solve this problem, in addition to the two-wire connection method, Pt100 also has three-wire and four-wire connection methods to reduce or even eliminate the measurement error caused by lead resistance.
As mentioned above, Pt100 is a resistive temperature sensor, and the essence of its temperature measurement is actually to measure the resistance of the sensor. The usual approach is to convert resistance into electrical signals such as voltage or current for measurement, and then use a microcontroller to linearize the measurement results. Generally, there are two options for temperature measurement using Pt100:
1. Design a constant current source to pass through the Pt100 thermal resistor, and calculate the temperature by detecting the voltage on the Pt100;
2. Use Wheatstone bridge. Three of the four resistances of the bridge are constant, and the other one uses a Pt100 thermal resistor. When the resistance value of Pt100 changes, an electric-heat difference will be generated at the test end, and the temperature is calculated from the electric-heat difference.
There is also a type of measurement method called "proportional method", which can be regarded as an improvement of the first type of measurement method and will be introduced in detail later.
The connection method of the 2-wire constant current source excitation is shown in the figure below. Pass the constant current source output through Pt100, measure the voltage across Pt100 and convert it into temperature. As mentioned before, this connection method will cause large errors when the Pt100 lead is long. Therefore, the more practical methods in actual applications are three-wire and four-wire connections.
The 4-wire connection method (Kelvin connection method) is shown in the figure below. Use two different sets of leads to lead out the excitation and measurement ends of Pt100. Since the voltage measurement point is at the lead connection of Pt100, the lead excitation voltage will not affect the measurement results.
The four-wire connection method is widely used in laboratory temperature measurement due to its high accuracy. However, due to constraints such as cost and wiring convenience, the three-wire connection method is more widely used in industrial control sites.
The figure below shows a typical connection method of a three-wire Pt100 excited by a constant current source. The basic principle is to assume that the three leads of Pt100 use the same type of cable with the same length and have the same resistance value, that is, Rw1=Rw2=Rw3 in the figure below, and use the measurement end (Rw2 lead) to compensate for the lead resistance.
Specifically, for the connection in the figure, the voltage at the non-inverting input terminal of op amp A3 is V+=Vpt100+VRw3, and the voltage at the inverting input terminal of op amp A3 is V-=VRw1 + Vpt100 + VRw3. Based on the assumption that Rw1=Rw2=Rw3, there is Vrw1 = Vrw3. Then the output Vo of op amp A3 = 2V+ - V- = Vpt100. That is to say, the influence of lead resistance on the measurement results is theoretically eliminated.
The Wheatstone bridge is another common connection method for Pt100. Its two-wire connection method is shown in the figure below. Obviously when the Pt100 lead is longer, larger errors will be introduced.
The three-wire Pt100 Wheatstone bridge connection method is shown in the figure below. The output formula of the Wheatstone bridge is as follows. If R3=Rpt100 is selected, the measurement error caused by the lead resistance can be theoretically eliminated.
4. 2, 3, and 4-wire connection methods in proportional method measurement
The essence of the proportional method measurement is to connect Pt100 in series with a reference resistor and apply an excitation source. Since the current flowing through the Pt100 and the reference resistor is the same, the voltage ratio between the two is the ratio of the resistance values. Taking the voltage across the reference resistor as the AD converter reference voltage and performing AD conversion on the voltage across the Pt100, there is the formula where D is the ADC conversion result and N is the number of ADC bits.
Since the current flowing through the Pt100 and the reference resistor is the same, compared with the above two structures, this circuit has lower requirements for the excitation source. Due to its simple structure, few precision components, and high measurement accuracy, proportional method measurement circuits are recognized by more and more people.
The figure below shows the proportional two-wire Pt100 connection method. Obviously when the Pt100 lead is longer, larger errors will be introduced.
In this circuit, the two-wire Pt100 can be directly replaced with the four-wire Pt100 and changed to a four-wire connection to eliminate lead errors.
The figure below shows the proportional three-wire Pt100 connection method. Use two constant current sources with equal outputs to compensate for lead resistance.
