Parameters of PT100 and PT1000 Platinum Resistance Sensors
Temperature detection has been widely used in our daily life and industrial sites. The accuracy of temperature measurement circuits is becoming more and more important. How to improve the accuracy of temperature measurement circuits? This article will take the temperature measurement solution of PT100 thermal resistance sensor as an example. Starting from the selection parameters of thermal resistors, I will briefly explain the direction of improving temperature measurement accuracy.
Platinum thermal resistance has good long-term stability and accuracy and is a commonly used industrial temperature measurement sensing element. In recent years, the thin film printing production process has reduced the use of precious metal platinum, and the cost of platinum thermal resistors has dropped significantly, and it has gradually been widely used. When using the platinum thermal resistor with the subsequent circuit, pay attention to its three basic parameters: nominal resistance, temperature coefficient, and accuracy level. We can decide the selection of platinum thermal resistor. Understanding the temperature resistance conversion characteristics, measurement current, and wiring methods can help us introduce as little additional circuit errors as possible and build an accurate temperature measurement circuit.
1. Nominal resistance
The nominal resistance is the resistance value of the platinum thermal resistor at the freezing point of 0°C. PT100 with a nominal resistance of 100Ω is the most commonly used, and there are also PT200, PT500, and PT1000 with nominal resistances of 200Ω, 500Ω, and 1000Ω.
2. Temperature coefficient
The temperature coefficient TCR is the average change in resistance per unit temperature of a platinum thermal resistor between the freezing point and boiling point of water. Different organizations use different temperature coefficients as their standards. The temperature coefficient adopted by European IEC60751 and Chinese GB/T30121 is 0.003851. The temperature coefficient adopted by ASTM E1137 in the United States is 0.003902, and 0.003851 is currently the industry standard recognized domestically and in most countries.
The calculation process of temperature coefficient is as follows, taking PT100 as an example.
TCR= (R100-R0)/(R0×100)
The resistance value R100=138.51Ω when the boiling point is 100℃, and the resistance value R0=100Ω when the freezing point is 0℃. Divide the difference 38.51 by the nominal resistance and then divide by 100°C. The result is the average temperature coefficient.
3. Accuracy level
IEC60751 stipulates the accuracy level and allowable error of platinum thermal resistors. Taking the A-class platinum thermal resistor as an example, the maximum temperature error consists of two parts. The fixed error caused by the deviation of the nominal resistance value at 0℃ is 0.15℃, plus the error introduced by the temperature coefficient drift is 0.002×|T|. where T is the actual temperature measurement range. When T does not exceed the application temperature range -30~+300℃ in the accuracy grade table, the platinum thermal resistance does not exceed the allowable error of the accuracy grade.
When the measured temperature is 100℃, the total error of Class A platinum thermal resistor is 0.15+0.002×100=0.35℃. When selecting a model, the nominal resistance, temperature coefficient standard, accuracy grade and application temperature range of the platinum thermal resistor are the basis for our selection.
4. Temperature resistance conversion characteristics
The temperature resistance conversion relationship of platinum thermal resistance is described by the following formula, which is divided into two situations: below 0℃ and above 0℃.
When T≤0℃: RT=R0• (1+A•T+B•T2+C• (T-100℃) •T3)
When T≥0℃: RT=R0• (1+A•T+B•T2)
Among them, RT is the resistance value at temperature T, and R0 is the resistance value at 0°C. A, B, and C are the three constants specified in IEC60751, and their values are 3.9083×10-3 °C-1, -5.775×10-7 °C-2, and -4.183×10-12 °C-4 respectively. The measured temperature T can be solved by directly substituting the resistance value RT into the formula, but it requires solving a cubic equation and the calculation is complicated.
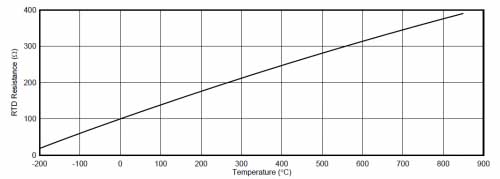
In order to simplify the calculation, use the formula to output the temperature resistance value curve of PT100 in the range of -200~+850°C, as shown below. The resistance value of PT100 changes in the range of 18~400Ω, and has an approximately linear temperature resistance value conversion relationship.
If you use the two endpoints of -200°C and +850°C to directly perform a two-point linear calibration, try to simplify the calculation. The temperature resistance value curve within the temperature range is as shown below. At this time, the maximum nonlinear error exceeds 16Ω, and the error is relatively large.
Generating a temperature resistance value table based on the formula, and then performing small-range linear interpolation in the lookup table, is a method that is both simple to calculate and can achieve accurate approximation. A lookup table of temperature resistance values with intervals of 1°C is attached in IEC60751.
5. Measure the current
Platinum resistance thermometers are almost always measured using DC current excitation. Measuring current inevitably generates heat in the resistor, introducing self-heating errors. The platinum thermal resistance manual has two parameters: measurement current and self-heating coefficient. The typical measurement current I is 0.3~1mA, and the self-heating coefficient S is about 0.015℃/mW.
The temperature error introduced by the measurement current can be calculated based on the self-heating coefficient, according to the following formula.
ΔT = P×S=(I2×R) ×S
For example, given 1mA, when the maximum resistance of PT100 is 400Ω, the self-heating temperature generated is about 0.01℃. In this case the error is almost negligible. When the self-heating coefficient of the platinum resistance is not affected, the measurement current is set to the maximum value first. When the current is too small, the amplitude of the output voltage becomes smaller and the signal-to-noise ratio decreases. 1mA is a commonly used measurement current value.
6. Wiring method
The output lead methods of platinum thermal resistance include two-wire system, three-wire system and four-wire system. The error introduced by the two-wire lead resistance cannot be eliminated. The four-wire system has no lead resistance error, but has the largest number of leads. The three-wire system is based on the fact that the resistance values of the three leads are equal under the same physical size conditions. The lead error can be eliminated by calculation after measuring the resistance value twice, which is the most commonly used method.
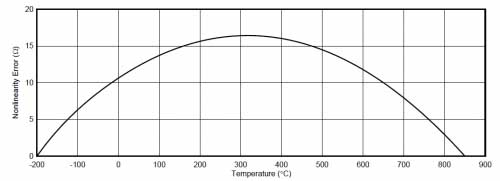Figure 5, Platinum thermal resistor wiring method
7. Summary
The accuracy of the temperature measurement circuit requires not only the early selection of the thermal resistor, but also the subsequent optimization of hardware design and software algorithm. Yaxun Electronics provides the PT100 interface module TPS02 with a three-wire interface for platinum thermal resistance measurement. It has a high-stability measurement circuit including built-in excitation current source, 24-bit ADC, resistance temperature value linearization algorithm, 2500V electrical isolation, and the temperature value can be read through the IIC digital interface by connecting a platinum thermal resistor.
1. Nominal resistance
The nominal resistance is the resistance value of the platinum thermal resistor at the freezing point of 0°C. PT100 with a nominal resistance of 100Ω is the most commonly used, and there are also PT200, PT500, and PT1000 with nominal resistances of 200Ω, 500Ω, and 1000Ω.
2. Temperature coefficient
The temperature coefficient TCR is the average change in resistance per unit temperature of a platinum thermal resistor between the freezing point and boiling point of water. Different organizations use different temperature coefficients as their standards. The temperature coefficient adopted by European IEC60751 and Chinese GB/T30121 is 0.003851. The temperature coefficient adopted by ASTM E1137 in the United States is 0.003902, and 0.003851 is currently the industry standard recognized domestically and in most countries.
The calculation process of temperature coefficient is as follows, taking PT100 as an example.
The resistance value R100=138.51Ω when the boiling point is 100℃, and the resistance value R0=100Ω when the freezing point is 0℃. Divide the difference 38.51 by the nominal resistance and then divide by 100°C. The result is the average temperature coefficient.
3. Accuracy level
IEC60751 stipulates the accuracy level and allowable error of platinum thermal resistors. Taking the A-class platinum thermal resistor as an example, the maximum temperature error consists of two parts. The fixed error caused by the deviation of the nominal resistance value at 0℃ is 0.15℃, plus the error introduced by the temperature coefficient drift is 0.002×|T|. where T is the actual temperature measurement range. When T does not exceed the application temperature range -30~+300℃ in the accuracy grade table, the platinum thermal resistance does not exceed the allowable error of the accuracy grade.
When the measured temperature is 100℃, the total error of Class A platinum thermal resistor is 0.15+0.002×100=0.35℃. When selecting a model, the nominal resistance, temperature coefficient standard, accuracy grade and application temperature range of the platinum thermal resistor are the basis for our selection.
4. Temperature resistance conversion characteristics
The temperature resistance conversion relationship of platinum thermal resistance is described by the following formula, which is divided into two situations: below 0℃ and above 0℃.
When T≤0℃: RT=R0• (1+A•T+B•T2+C• (T-100℃) •T3)
When T≥0℃: RT=R0• (1+A•T+B•T2)
Among them, RT is the resistance value at temperature T, and R0 is the resistance value at 0°C. A, B, and C are the three constants specified in IEC60751, and their values are 3.9083×10-3 °C-1, -5.775×10-7 °C-2, and -4.183×10-12 °C-4 respectively. The measured temperature T can be solved by directly substituting the resistance value RT into the formula, but it requires solving a cubic equation and the calculation is complicated.
In order to simplify the calculation, use the formula to output the temperature resistance value curve of PT100 in the range of -200~+850°C, as shown below. The resistance value of PT100 changes in the range of 18~400Ω, and has an approximately linear temperature resistance value conversion relationship.
If you use the two endpoints of -200°C and +850°C to directly perform a two-point linear calibration, try to simplify the calculation. The temperature resistance value curve within the temperature range is as shown below. At this time, the maximum nonlinear error exceeds 16Ω, and the error is relatively large.
Generating a temperature resistance value table based on the formula, and then performing small-range linear interpolation in the lookup table, is a method that is both simple to calculate and can achieve accurate approximation. A lookup table of temperature resistance values with intervals of 1°C is attached in IEC60751.
5. Measure the current
Platinum resistance thermometers are almost always measured using DC current excitation. Measuring current inevitably generates heat in the resistor, introducing self-heating errors. The platinum thermal resistance manual has two parameters: measurement current and self-heating coefficient. The typical measurement current I is 0.3~1mA, and the self-heating coefficient S is about 0.015℃/mW.
The temperature error introduced by the measurement current can be calculated based on the self-heating coefficient, according to the following formula.
For example, given 1mA, when the maximum resistance of PT100 is 400Ω, the self-heating temperature generated is about 0.01℃. In this case the error is almost negligible. When the self-heating coefficient of the platinum resistance is not affected, the measurement current is set to the maximum value first. When the current is too small, the amplitude of the output voltage becomes smaller and the signal-to-noise ratio decreases. 1mA is a commonly used measurement current value.
6. Wiring method
The output lead methods of platinum thermal resistance include two-wire system, three-wire system and four-wire system. The error introduced by the two-wire lead resistance cannot be eliminated. The four-wire system has no lead resistance error, but has the largest number of leads. The three-wire system is based on the fact that the resistance values of the three leads are equal under the same physical size conditions. The lead error can be eliminated by calculation after measuring the resistance value twice, which is the most commonly used method.
7. Summary
The accuracy of the temperature measurement circuit requires not only the early selection of the thermal resistor, but also the subsequent optimization of hardware design and software algorithm. Yaxun Electronics provides the PT100 interface module TPS02 with a three-wire interface for platinum thermal resistance measurement. It has a high-stability measurement circuit including built-in excitation current source, 24-bit ADC, resistance temperature value linearization algorithm, 2500V electrical isolation, and the temperature value can be read through the IIC digital interface by connecting a platinum thermal resistor.
